Cryptopals set 2
These are my solutions for the second set of the cryptopals challenge, which focus on block cipher cryptography. As for the first set, you can find the complete solutions on the same repo.
List of challenges:
09. Implement PKCS#7 padding
In this exercise we have to implement a padding scheme, in particular the PKCS#7, described here.
There isn't much to say about this exercise, the RFC describes how to do it.
def pad_pkcs7(message: bytes, bsize: int) -> bytes:
"""pad_pkcs7: pad the message to the blocksize specified by bsize using
the PKCS#7 padding scheme.
https://tools.ietf.org/html/rfc5652#section-6.3
:param message: the message to pad.
:type message: bytes
:param bsize: the block size to use
:type bsize: int
:return: the padded message
:rtype: bytes
"""
if bsize<2 or bsize>255:
raise ValueError
mlen = len(message)
pad_size = bsize - (mlen % bsize)
pad_val = pad_size.to_bytes(1, sys.byteorder, signed=False)
padding = pad_val * pad_size
return message + padding
10. Implement CBC mode
CBC (Cipher Block Chaining) is another block cipher mode (like ECB) and one of the most used. We saw in the set 1 that ECB can be dangerous to use, to avoid the this problems, CBC "randomise" the plaintext by XORing each plaintext block with the previous ciphertext block:
For the first block of plaintext (that do not have a previous ciphertext block to get XORed against) it is used an Initialisation Vector (IV). There are different ways to generate an IV but let's use a fixed one in this case. The decryption works this way:
For this exercise we have to implement both the encryption and the decryption of the CBC mode, reusing some code previously written (ECB function, padding, etc..). To test if our code works, we have to decrypt a file (encoded in base64), given the key and the IV.
Here is the code just for CBC decryption, you can find the encryption function in the repo:
def decrypt_AES_128_CBC(ciphertext: bytes, key: bytes, iv: bytes) -> bytes:
"""decrypt_AES_128_CBC
:param ciphertext: the ciphertext to decrypt
:type ciphertext: bytes
:param key: the key
:type key: bytes
:param iv: initialisation vector
:type iv: bytes
:return: the plaintext unpadded
:rtype: bytes
"""
# block size is 128 bits (16 bytes)
bsize = 16
ctlen = len(ciphertext)
plaintext = bytes()
# start the decryption
# the first block is XORed with the IV
ciph_block = ciphertext[:bsize]
# decrypt the block
pt_tmp = decrypt_AES_128_ECB(ciph_block, key)
# XOR against IV and append to final plaintext
plaintext += fixed_xor(pt_tmp, iv)
# loop the remaining blocks
for i in range(1, ctlen//bsize):
# the ciphertext block about to get decrypted
ciph_block = ciphertext[i*bsize:i*bsize+bsize]
# decrypt the block
pt_tmp = decrypt_AES_128_ECB(ciph_block, key)
# XOR the plaintext against the previous ciphertext block and append to
# the final plaintext
plaintext += fixed_xor(pt_tmp,
ciphertext[(i-1)*bsize:(i-1)*bsize+bsize])
# unpad the plaintext
plaintext = unpad_pkcs7(plaintext, bsize)
return plaintext
The decrypted file contains the lyrics of "Vanilla Ice - Play that Funky Music".
11. An ECB/CBC detection oracle
For this exercise we have to find a way to detect whether a ciphertext was obtained using ECB or CBC.
We have already seen in set1 that if we use the ECB mode and we encrypt the same vaules with the same key we end up with same ciphertext. In this case we have the complication of the two random strings of random size that are appended before and after the plaintext. We have to find a way to craft our input in such a way that the the same key will end up encrypting blocks containing the same values. If we manage to do it we know that, if ECB is being used, we will find two equal blocks in the ciphertext. The plaintext that will get encrypted will have this structure:
|rand bits | choosen plaintext |rand bits |
-------------------------------------------------------------------------
|<-5 to 10 bytes->|<- we can decide the size ->|<-5 to 10 bytes->|
-------------------------------------------------------------------------
|<- 16 bytes ->|<- 16 bytes ->|<- 16 bytes ->|<- 16 bytes ->|
-------------------------------------------------------------------------
|??| |??|
We have random values at the beginning and end of the plaintext that we do not control, with a variable length between 5 to 10 bytes; between those there is the portion of the plaintext that we can decide. We have to make sure that our crafted plaintext will end up filling at least two blocks with the same value. Since the size of the random bytes is variable we don't know how much it will fill the first (and last) block. Since the length goes between 5 and 10, to fill completly the first block we'll need between 11 (16-5=11) or 6 (16-10=6) bytes. On top of that we have to fill at least two other blocks (32 bytes) with the same value. So to be sure to have two blocks completely filled with the same value we'll need 32+11=43 bytes.
def encryption_oracle(plaintext: bytes) -> (bytes, str):
"""encryption_oracle: an encryption oracle that:
+ append before the given plaintext a random value buffer of random size
between 5 and 10 bytes.
+ append after the given plaintext a random value buffer of random size
between 5 and 10 bytes.
+ use randomly (0.5 probability each) AES 128 CBC or AES 128 ECB
+ generate a random key
+ generate a random IV
Returns a tuple containing the ciphertext and a string that state the block
mode used:
+ 0 for ECB
+ 1 for CBC
:param bytes: the plaintext
:param str:
:rtype: (bytes,str)
"""
rng = SystemRandom()
pre_size = rng.randrange(5,11)
pre = generate_random_bytes(pre_size)
post_size = rng.randrange(5,11)
post = generate_random_bytes(post_size)
plaintext = pre + plaintext + post
key = generate_random_bytes(16)
mode = rng.randrange(0,2)
if mode == 0:
# use ECB
plaintext = pad_pkcs7(plaintext, 16)
ciphertext = encrypt_AES_128_ECB(plaintext, key)
elif mode == 1:
#use CBC
iv = generate_random_bytes(16)
ciphertext = encrypt_AES_128_CBC(plaintext, key, iv)
else:
raise Exception
return ciphertext, mode
def detect_enc_mode(oracle: encryption_oracle, min_plain_size: int) -> int:
bsize = 16
plaintext = bytes(randrange(256))*min_plain_size
ciphertext, mode = encryption_oracle(plaintext)
blocks = find_repeating_blocks(ciphertext, bsize)
repeating = blocks.values()
for i in iter(repeating):
if i > 1:
return 0, mode
return 1, mode
if __name__ == '__main__':
for i in range(10):
min_plain_size = 43
guessed_mode, mode = detect_enc_mode(encryption_oracle, min_plain_size)
if guessed_mode == mode:
print('✓')
else:
print('✕')
print('-'*10)
12. Byte-at-a-time ECB decryption (Simple)
For this exercise, we have to rewrite the oracle function in such a way that the ciphertext \(C\) gets computed by encrypting a string made up by appending a secret text \(S\) to the plaintext \(P\) passed to the oracle function. Both \(S\) and key \(K\) used for the encryption are secret.
The oracle function will be something like this:
def encryption_oracle_ecb(plaintext: bytes) -> bytes:
"""encryption_oracle_ecb: encryption oracle using AES 128 with ECB and a
secret, constant key. Before encrypting, a secret string gets appended
after the plaintex.
Returns the ciphertext.
:param plaintext: the plaintext to encrypt, NOT padded
:type plaintext: bytes
:return: the ciphertext
:rtype: bytes
"""
secret = ('Um9sbGluJyBpbiBteSA1LjAKV2l0aCBteSByYWctdG9wIGRvd24gc28gbXkg'
'aGFpciBjYW4gYmxvdwpUaGUgZ2lybGllcyBvbiBzdGFuZGJ5IHdhdmluZyBq'
'dXN0IHRvIHNheSBoaQpEaWQgeW91IHN0b3A/IE5vLCBJIGp1c3QgZHJvdmUg'
'YnkK')
key = b'YELLOW SUBMARINE'
plaintext += base64.b64decode(secret)
plaintext = pad_pkcs7(plaintext, 16)
ciphertext = encrypt_AES_128_ECB(plaintext, key)
return ciphertext
What we get to know is \(C\) and \(P\) and we want to find \(S\). We'll see that once we guess the blocksize, if ECB cipher mode is used, we can find \(S\) without recovering the key \(K\).
Let's get the boring stuff out of the way and then move to the core of the challenge.
To check the block size of the cipher used in the oracle function we can pass to the oracle an increasing length plaintext, one byte at a time, and check when the length of the ciphertext change. The difference beteween the previous length is the block size.
def find_blocksize(oracle: encryption_oracle_ecb) -> (int, int):
"""find_blocksize: find the block size up to a maximum of 512 bits.
Returns a tuple of int containing the block size and the number of filling
characters entered to get a new block. If the blocksize was not found,
returns 0.
:param oracle:
:type oracle: encryption_oracle_ecb
:rtype: tuple
"""
# max block size to check for
bsize_max = 64
plaintext = b''
ciphertext = oracle(plaintext)
ct_len = len(ciphertext)
blocksize = 0
for i in range(bsize_max+1):
plaintext += b'A'
ciphertext = oracle(plaintext)
if len(ciphertext) != ct_len:
blocksize = len(ciphertext)-ct_len
break
return blocksize, i+1
Let's check if the cipher mode used is ECB by feeding the oracle two equal blocks in the plaintext and checking if there are two equal blocks in the ciphertext.
def test_ecb(oracle: encryption_oracle_ecb, bsize: int) -> bool:
"""test_ecb: test for ECB cipher mode by encrypting with the oracle
function two block with the same value and checking if the resulting
ciphertext have two equal blocks.
Return True if the mode is ECB, False otherwise.
:param oracle: the oracle function
:type oracle: encryption_oracle_ecb
:param bsize: the block size in byte to use
:type bsize: int
:return: True if ECB, False otherwise
:rtype: bool
"""
pt_same_2_block = b'A'*bsize*2
ct_same_2_block = encryption_oracle_ecb(pt_same_2_block)
blocks = find_repeating_blocks(ct_same_2_block, bsize)
ecb = False
for i in blocks.values():
if i > 1:
ecb = True
return ecb
Good, now we can detect the block size and if the oracle is using ECB cipher mode, let's see how \(S\) can be recovered.
For the sake of the explanation let \(S\) be \([s_0, s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_8, s_9]\), keeping in mind that we don't know it's value and let the block size be \(bsize=4\). Giving the oracle a plaintext crafted in such a way that its length is just one byte short of the block size (\(P_0=[p_0, p_1, p_2]\)), we end up with:
The following image help visualise what's going on.
|p0 p1 p2 s0 |s1 s2 s3 s4 |s5 s6 s7 s8 |
|k1 k2 k3 k4 |k1 k2 k3 k4 |k1 k2 k3 k4 |
----------------------------------------
|c0 c2 c3 c4 |c5 c6 c7 c8 |c9 c10 c11 c12|
If we focus on the first block we see that \(C_0=[c_0, c_1, c_2, c_3]\) is the result of encrypting \([p_0, p_1, p_2, s_0]\). Since we know \(P_0\), we can find \(s_0\) by making repeated call to the oracle function trying all possible value of \(s_0\) until we get a ciphertext whose first block corresponds to \(C_0\). In other words we are feeding the oracle a crafted plaintexts \(TP_0=[p_0, p_1, p_2, x_0]\) for every possible value of \(x_0\) until the first block \(oracle(TP_0)[0:4] = oracle(P_0)[0:4]\), for which \(x_0 = s_0\). Once we find \(x_0\) we managed to find the first byte \(s_0\) of the secret text.
We can clear the whole first block by repeating the steps before and reducing each time the length of the plaintext by one byte. For example, to get the second byte \(s_1\) we feed the oracle \(P_1=[p_0, p_1]\):
|p0 p1 s0 s1 |s2 s3 s4 s5 |s6 s7 s8 s9 |
|k1 k2 k3 k4 |k1 k2 k3 k4 |k1 k2 k3 k4 |
----------------------------------------
|c0 c2 c3 c4 |c5 c6 c7 c8 |c9 c10 c11 c12|
Since now we know \(s_0=x_0\) we are exactly in the same situation as before. We feed the oracle a crafted plaintext \(TP_1=[p_0, p_1, x_0, x_1]\) trying every possible value for x_1 until the first block of \(oracle(TP_1)\) and \(oracle(C_1)\) are equal, then we have found \(x_1=s_1\).
Once we're done with the first block we can move to the next ones, using the same strategy but instead of comparing the first block we look at the n-block. For example, with the second block we start again with \(P_0=[p_0, p_1, p_2]\) and
:
|p0 p1 p2 s0 |s1 s2 s3 s4 |s5 s6 s7 s8 |
|k1 k2 k3 k4 |k1 k2 k3 k4 |k1 k2 k3 k4 |
----------------------------------------
|c0 c2 c3 c4 |c5 c6 c7 c8 |c9 c10 c11 c12|
The difference is that this time we are interested in \(s_4\), since we have already recovered the first 4 bytes of \(S\) in \(X=[x_0, x_1, x_2, x_3]\), so now we're looking at the second block. We try again every possible value for \(x_4\) feeding the oracle function \(TP=[P_0|X|x_4]\) until we find \(x_4\) for which the second block of \(oracle(TP)\) is equal to the second block of \(oracle(P0)\).
Here is the code:
def byte_at_a_time_post(oracle: encryption_oracle_ecb, bsize: int) -> bytes:
"""byte_at_a_time_post
:param oracle:
:type oracle: encryption_oracle_ecb
:param bsize:
:type bsize: int
:rtype: bytes
"""
print('[+] Trying byte at a time attack:')
# store here the recovered bytes
recovered = bytearray()
# start with a plaintext one byte short of the blocksize
plaintext = b'A'*(bsize-1)
# compute how many blocks we have to crack
ciphertext = oracle(b'')
if len(ciphertext)%bsize != 0:
raise ValueError
n_blocks = int(len(ciphertext)/bsize)
# get the length of the secret text
bsize, filling = find_blocksize(encryption_oracle_ecb)
s_length = len(ciphertext)-filling
# compute just once all the plaintexts (P_n) and corresponding
# ciphertexts(C_n) then store them in ct_store
ct_store = {}
for i in range(bsize):
plaintext = b'A'*(bsize-1-i)
ciphertext = oracle(plaintext)
ct_store[i] = {}
ct_store[i]['C'] = ciphertext
ct_store[i]['P'] = plaintext
# decrypt one block at a time
for b in range(n_blocks):
# cycle through every byte in the block
for i in range(bsize):
# try every possible value [0, 255] in one byte
for k in range(256):
# craft the input using the current plaintext P_n, the bytes
# recovered so far and the current test value
crafted_input = ct_store[i]['P']+recovered+k.to_bytes(1, sys.byteorder)
# get the ciphertext using the crafted input
cipher_crafted = oracle(crafted_input)
# check if the b-th blocks of the two ciphers match
if (cipher_crafted[b*bsize:b*bsize+bsize] ==
ct_store[i]['C'][b*bsize:b*bsize+bsize]):
# if they match, we got a new byte. store it
recovered += k.to_bytes(1, sys.byteorder)
sys.stdout.write('\r recovered {0}/{1} bytes: {2}'.format(
len(recovered),
s_length,
repr(recovered.decode())
))
# check if we recovered all the characters
if len(recovered) == s_length:
sys.stdout.write('\n')
sys.stdout.flush()
#return the secret string
return recovered
# exit the bruteforce loop
break
And here's the output with the recovered secret text \(S\):
$ python ch12.py
[+] Block size: 16
[+] ECB mode: True
[+] Trying byte at a time attack:
recovered 138/138 bytes: "Rollin' in my 5.0\nWith my rag-top down so my hair
can blow\nThe girlies on standby waving just to say hi\nDid you stop? No, I
just drove by\n"
13. ECB cut-and-paste
For this exercise I'm assuming that the attacker knows how the encoding works.
To get around the routine that sanitise the input and obtain an admin role, we can
generate different ciphertexts using the profile function and than, as the
title suggests, cut and paste the ciphertexts in such a way that, once decrypted,
we get the desired plaintext. The goal is to craft a ciphertext whose plaintext
will have the role field set to admin.
As a reminder, the encoded profile has this structure: email=foo@bar.com&uid=10&role=user.
Since ECB is being used, every blocks is encrypted indipendently by the others and with the same, so we can shuffle around the blocks in the ciphertext and we will end up with a plaintext with the corresponding blocks moved around. If \(C\) is the original ciphertext with \(4\) blocks \(c_n\): \(C=[c_0, c_1, c_2, c_3, c_4]\) and we move the blocks around \(C_{shuffle}=[c_2, c_4, c_1, c_3]\) the result of the decryption \(P_{shuffle} = D(C_{shuffle}, K)\) will be \(P_{shuffle}=[p_2, p_4, p_1, p_3]\).
Since we can cut only at multiple of the blocksize, a convenient way to reach our goal is to get the ciphertext blocks of the following plaintext:
|email=jerry@nsa.|gov&uid=10&role=|admin___________|
To get the last block we have to craft the email so that the first block gets
filled and then append the string
"admin0x110x110x110x110x110x110x110x110x110x110x11", the 0x11 is the
padding since \(16 - len('admin') = 11\).
# get the block containing the string admin followed by the padding
# (11 bytes)
val = 11
fill = val.to_bytes(1, sys.byteorder)*val
# 'me@nsa.gov' fills the first block the rest will be in the second block
crafted = 'me@nsa.govadmin'+fill.decode()
# get the ciphertext
c1 = profile_for(crafted)
# pick the second block
c11 = c1[16:32]
To obtain the firtst two blocks we just create a profile for jerry@nsa.gov
and then discard the last block
# create the profile for jerry@nsa.gov
c2 = profile_for('jerry@nsa.gov')
# cut the first two blocks
c21 = c2[:32]
# paste the blocks
ciphertext = c21+c11
# get the encoded profile with admin role in plaintext
plaintext = parse_key_val(ciphertext)
And we're done, if we print the plaintext we get:
python ch13.py
{'uid': '10', 'email': 'jerry@nsa.gov', 'role': 'admin'}
14. Byte-at-a-time ECB decryption (Harder)
This exercise is similar to the number 12, with a slight difference that now the oracle function also prepend a random string of random values \(R\) to the plaintext. Keeping the same meaning for the others variables, the oracle can be described as:
We can reuse the same strategy and almost the same code of exercise 12 by noticing that if we make sure that the last block of the random text is completely filled, the problem is exactly the same, we just have to skip the initial blocks containing the random string \(R\).
This is what we need:
- the number of bytes needed to fill the last block used by the random string \(R\)
- the number of blocks (after the "filling") used by \(R\)
- obviously we need the blocksize of the ciphertext
And here's how to get those values:
# get the blocksize used by the oracle
bsize, fill = find_blocksize(encryption_oracle_ecb_pre_post)
filling = b'A'
# give an increasing length input to the oracle until you fill completely
# two blocks (ECB is used, you'll find two equal blocks in the cipher)
while True:
ciphertext = encryption_oracle_ecb_pre_post(filling)
blocks = find_repeating_blocks(ciphertext)
if 2 in blocks.values():
for b,n in blocks.items():
if n == 2:
block = b
break
break
filling += b'A'
# this is the how much space of its last block is NOT used by the random prefix
# because it doesn't match the blocksize
fill_len = len(filling) - bsize*2
# here's where the two filled blocks start (first position after the
# "filled" blocks used by the random prefix)
position = ciphertext.find(block+block)
recovered = byte_at_a_time_pre_post(encryption_oracle_ecb_pre_post, bsize,
fill_len, position)
Now we modify slightly the byte_at_a_time function of exercise 12, this time
the function takes two additional parameters that we just calculated: the
fill_len and the position. We use fill_len to fill completely the blocks
used by the random prefix and the position value to offset the comparison of
the blocks. Note the also the find_blocksize function has to be slightly
modified to take in consideration the fill_len
def find_blocksize(oracle, fill_len=0) -> (int, int):
"""find_blocksize: find the block size up to a maximum of 512 bits.
Returns a tuple of int containing the block size and the number of filling
characters entered to get a new block. If the blocksize was not found,
returns 0.
:param oracle:
:type oracle: encryption_oracle_ecb
:rtype: tuple
"""
# max block size to check for
bsize_max = 64
plaintext = b'A'*fill_len
ciphertext = oracle(plaintext)
ct_len = len(ciphertext)
blocksize = 0
for i in range(bsize_max+1):
plaintext += b'A'
ciphertext = oracle(plaintext)
if len(ciphertext) != ct_len:
blocksize = len(ciphertext)-ct_len
break
return blocksize, i+1
def byte_at_a_time_pre_post(oracle: encryption_oracle_ecb_pre_post, bsize: int,
fill_len: int, pre_position: int) -> bytes:
"""byte_at_a_time_post
:param oracle:
:type oracle: encryption_oracle_ecb
:param bsize:
:type bsize: int
:rtype: bytes
"""
print('[+] Trying byte at a time attack:')
# fill the last block used by the random prefix to reach a full bsize block
fill = b'A' * fill_len
# store here the recovered bytes
recovered = bytearray()
# start with a plaintext one byte short of the blocksize
plaintext = b'A'*(bsize-1)
# add the filling
plaintext = fill + plaintext
# compute how many blocks we have to crack
ciphertext = oracle(fill+b'')
if len(ciphertext)%bsize != 0:
raise ValueError
n_blocks = int(len(ciphertext)/bsize)
# subtract the blocks used by the random prefix
n_blocks = n_blocks - pre_position//bsize
# get the length of the secret text, need to offset this with fill_len
bsize, filling = find_blocksize(oracle, fill_len)
# this is the length of the secret string
s_length = len(ciphertext)-filling-pre_position
# compute just once all the plaintexts (P_n) and corresponding
# ciphertexts(C_n) then store them in ct_store
ct_store = {}
for i in range(bsize):
plaintext = b'A'*(bsize-1-i)
plaintext = fill + plaintext
ciphertext = oracle(plaintext)
ct_store[i] = {}
ct_store[i]['C'] = ciphertext
ct_store[i]['P'] = plaintext
# decrypt one block at a time
for b in range(n_blocks):
# cycle through every byte in the block
for i in range(bsize):
# try every possible value [0, 255] in one byte
for k in range(256):
# craft the input using the current plaintext P_n, the bytes
# recovered so far and the current test value
crafted_input = ct_store[i]['P']+recovered+k.to_bytes(1, sys.byteorder)
# get the ciphertext using the crafted input
cipher_crafted = oracle(crafted_input)
# check if the b-th blocks of the two ciphers match
if (cipher_crafted[b*bsize+pre_position:b*bsize+pre_position+bsize] ==
ct_store[i]['C'][b*bsize+pre_position:b*bsize+pre_position+bsize]):
# if they match, we got a new byte. store it
recovered += k.to_bytes(1, sys.byteorder)
sys.stdout.write('\r recovered {0}/{1} bytes: {2}'.format(
len(recovered),
s_length,
repr(recovered.decode())
))
# check if we recovered all the characters
if len(recovered) == s_length:
sys.stdout.write('\n')
sys.stdout.flush()
#return the secret string
return recovered
# exit the bruteforce loop
break
This version of the byte_at_a_time attack is a generalisation of the previous one, it'll work even if no string is prepended to the user input.
And here's the output:
$ python ch14.py
[+] Trying byte at a time attack:
recovered 138/138 bytes: "Rollin' in my 5.0\nWith my rag-top down so my hair
can blow\nThe girlies on standby waving just to say hi\nDid you stop? No, I
just drove by\n"
15. PKCS#7 padding validation
For this exercise we modify the unpad function that we already wrote to add some validation of the padding. There are some test cases in the repo if you want to take a look, here's the code instead.
def unpad_pkcs7(message: bytes) -> bytes:
"""unpad_pkcs7: unpad the message using PKCS#7.
Return the unpadded message as bytes.
Raise ValueError if the padding is not valid.
:param message:
:type message: bytes
:rtype: bytes
"""
# get the last padding value
pad_val = int.from_bytes(message[-1:], sys.byteorder)
# count how many bytes with pad_val value are contained in the last pad_val
# bytes of the message
pad_num = message.count(message[-1:], -pad_val)
# check if the number of pad_val bytes and pad_val are the same
if pad_num != pad_val:
raise ValueError
return message[:-pad_val]
16. CBC bitflipping attacks
Let's have a look at how CBC decryption works, I took this image from wikipedia:
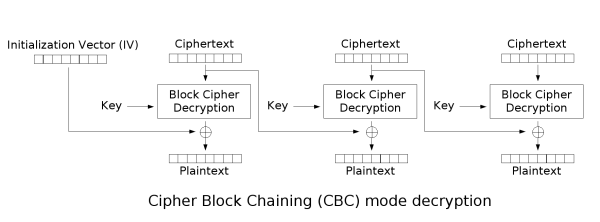
As said in the exercise, there are two important things to notice:
- by editing one ciphertext block, the corresponding plaintext block will be destroyed
- the other effect of changing bits in one ciphertext block, is that the next block plaintext will be XORED against a different value, effectively flipping the plaintext bits
The strategy used to complete this exercise is:
- Find out how long the random prefix is.
-
Craft the attacker controlled plaintext in such a way that it will:
- fill completely one block with a known value, I'll refer to this block as "empty block"
- fill the adiacent block with the target value. In our case the target value is the string we're trying to inject, replacing the forbidden values that will otherwise be eaten by the sanitisation function with some known values.
-
Encrypt the crafted plaintext
- Flip the right bits in the "empty block" ciphertext in such way that when decrypting the modified ciphertext we'll get the desired output in the "target block" plaintext.
How do we know which bits we have to flip? We know the position of the bytes in the "target block" we want to change, so we have to change the corresponding bytes in the "empty block". The value of the bytes in the empty block that will lead to our desired result can be found using this equation, here \(p1\) is the position in the block where we want to change the value:
So to get the right value to substitute in the ciphertext we have to XOR the ciphertext byte in the empty block with the plaintext in the target block and XOR it again with the value we want to see in the plaintext.
Here's the commented code, I left out all the oracle functions, you can find them in the repo as usual.
if __name__ == '__main__':
bsize = 16
# start with an empty input and see the difference with a one-byte input,
pad = b''
ciphertext_prev = oracle_encryption_cbc(pad)
pad = b'a'
ciphertext_step = oracle_encryption_cbc(pad)
# get the number of complete blocks are used by the random prefix
xored = cryptopals.xor_buf(ciphertext_prev, ciphertext_step)
start_equal_bytes = count_consecutive_zeros(xored)
start_eq_blocks = start_equal_bytes//bsize
ciphertext_prev = ciphertext_step
# increment the input to see if the random prefix is partially using
# another block
while True:
pad += b'a'
ciphertext_step = oracle_encryption_cbc(pad)
xored = cryptopals.xor_buf(ciphertext_prev, ciphertext_step)
# get how many blocks and bytes are not changed from the previous input
equal_bytes = count_consecutive_zeros(xored)
eq_blocks, eq_bytes = (equal_bytes//bsize, equal_bytes%bsize)
# if we filled another block we have to stop
if eq_blocks - start_eq_blocks >= 1:
pad = pad[:-1]
print('added {0} bytes'.format(len(pad)))
break
ciphertext_prev = ciphertext_step
# this is out target block, the 'X'es are the character where the forbidden
# characters would go
dummy = b'X'
target = b'aaaaa'+dummy+b'admin'+dummy+b'true'
# the offsets of the forbidden characters
o1 = 5
o2 = 11
# if the padding is 16 bytes it means that the random prefix was a multiple
# of the blocksize and we already have one "empty block"
if len(pad)==16:
# the position of the bytes to change
p1 = start_eq_blocks*bsize+o1
p2 = start_eq_blocks*bsize+o2
plaintext = pad + target
# otherwise we just filled a partially used block and we need to add the
# "empty block"
else:
# the position of the bytes to change
p1 = eq_blocks*bsize+o1
p2 = eq_blocks*bsize+o2
plaintext = pad + b'a'*bsize + target
# get the ciphertext using the crafted input
ciphertext = bytearray(oracle_encryption_cbc(plaintext))
# change the value of the ciphertext in order to obtain the desired values
# once decrypted
ciphertext[p1] = ciphertext[p1]^ord('X')^ord(';')
ciphertext[p2] = ciphertext[p2]^ord('X')^ord('=')
# check if we got the desired string in the plaintext
plain_tmp = oracle_decryption_cbc_match(bytes(ciphertext))
if plain_tmp == True:
print("Admin flag true")
Here's the output:
$ python ch16.py
added 16 bytes
b'comment1=cooking'|b'%20MCs;userdata='|b'\xe3\x05j\xc1\xd5\x12y\\P\x11\xc3\x1b\x8e\xc5#\xfb'|b'aaaaa;admin=true'|b';comment2=%20lik'|b'e%20a%20pound%20'|b'of%20bacon\x06\x06\x06\x06\x06\x06'|
Admin flag true